問題 (2025/08 東大レベル模試 3)
(1) 以下の条件を満たす正の整数 ${m}$ を小さい順番に $4$ つ求めよ : $$ | (1+i)^{m} + (1-i)^{m} | >10^{4} $$
(2) 以下の条件を満たす正の整数 ${m}$ を小さい順番に $4$ つ求めよ : $$ | (1+i)^{m} + (1-i)^{m+3} | >10^{4} $$ ただし, $2^{20}=1048576$ を使って良い.
東進の解答
$\alpha = 1+i$ として, $\alpha = \sqrt{2} \cos(\pi/4)$ を使ってうまくやっているが, (2)の変形はしんどいと思った.
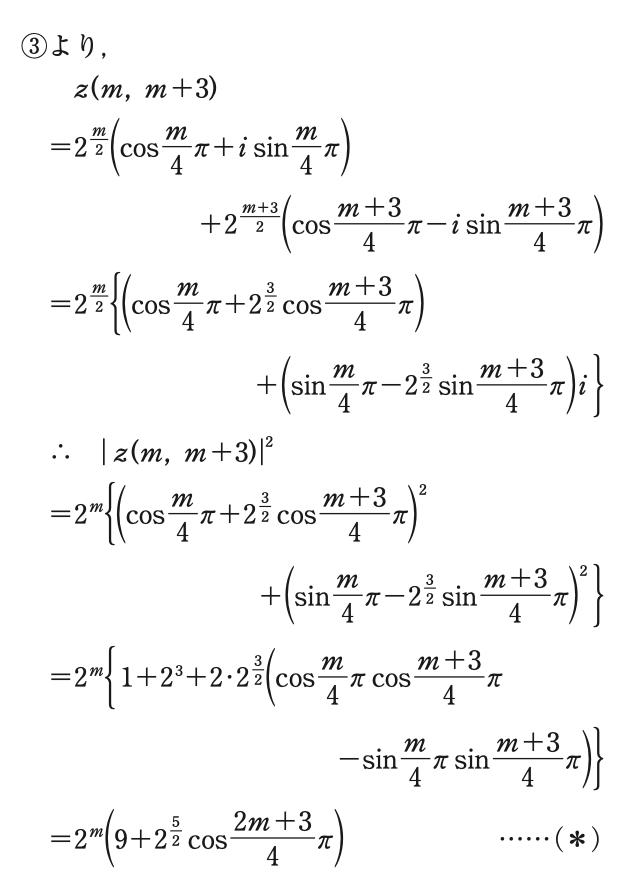
定理
$x^{2}-ax+b=0$ の解が $\alpha$, $\beta$ で, $\alpha \neq \beta$ であるとする.
数列 ${ x_{n} }$ が漸化式 $$ x_{n+2} - ax_{n+1} + bx_{n} = 0 \quad (n=0,1,2\ldots ) $$ を満たすとき, $x_{n}$の一般(一般)解は $\alpha$, $\beta$ と任意の定数 $c_1, c_2$ を用いて$$ x_{n} = c_1 \alpha^{n} + c_2 \beta^{n} $$ と表せる.
証明
ある数列 $x_{n}$ が漸化式を満たしているとして, それと等しい数列 $x'_n=c_1 \alpha^{n} + c_2 \beta^{n}$ の一般解を与えることを考える.
まず, $x_{0}$, $x_{1}$から $$ c_1 =\frac{x_1-\beta x_0}{\alpha-\beta}, \quad c_2 = \frac{x_1-\alpha x_0}{\beta-\alpha} $$ とすると, $x_0=x'_0$, $x_1=x'_1$ である. 次に, 帰納的に $x_{k}=x'_{k}$, $x_{k+1}=x'_{k+1}$ として, $\alpha$, $\beta$ が $x^{2}-ax+b=0$ の解であることを使うと \begin{aligned} x'_{k+2} &= c_1 \alpha^{k+2} + c_2 \beta^{k+2} \\ &= c_1 \alpha^{k} \alpha^{2} + c_2 \beta^{k} \beta^{2} \\ &= c_1 \alpha^{k} (a\alpha +b) + c_2 \beta^{k} (a\alpha +b) \\ &= a(c_1 \alpha^{k+1} + c_2 \beta^{k+1} ) + b(c_1 \alpha^{k}+c_2 \beta^{k}) \\ &= ax'_{k+1} + bx'_{k} \\ &= ax_{k+1} + bx_{k} \\ &= x_{k+2} \end{aligned} より, $x_{k+2} = x'_{k+2}$ が言えた. なので, ある数列が漸化式を満たすならこの形式で表せることが言えた.
逆に, 任意の $c_1, c_2$に対して $x_n = c_1 \alpha^{n} + c_2 \beta^{n}$ としたときそれが漸化式を満たすことはすぐわかるので, 証明できた.
つまり?
まず漸化式について, $x_n = \alpha^{n}$ は"特殊解"と呼ばれ, これはもちろん漸化式を満たします. 次に漸化式を満たす数列$x_n$と定数$c$について, その定数倍 $x'_n = cx_n$ の数列も漸化式を満たします. 次に漸化式を満たす数列 $x_n$, $x'_n$ について, その和 $x''_n = x_n + x'_n$ の数列も漸化式を満たします.
このようにして, 漸化式の解として満たされる全ての数列の集合を考えることができます.
これは微分方程式と似ています : $$\dfrac{d^{2}x}{dt^{2}}-a\dfrac{dx}{dt}+bx=0$$
もとの問題の解答
$\alpha = 1+i$, $\beta = 1-i$ とすると, これらは二次方程式 $$ z^{2} - 2z + 2 =0 $$ の解である.
(1) は, 数列 $z_{m}$ を $$ z_m = (1+i)^{m} + (1-i)^{m} = \alpha ^{m} + \beta^{m} $$ と定めると, 定理と同じ計算から $$ z_{m+2} = 2z_{m+1} -2 z_{m} $$ がわかる.
これを用いて, $z_0$, $z_1$ から, $z_{m}$ を地道に $m=30$ ぐらいまで計算すると (1) がわかるが, 周期 $8$ に注目してもいい. (省略)
(2) は, 再び $$ u_m = (1+i)^{m} + (1-i)^{m+3} = \alpha ^{m} + \beta^{3} \beta^{m} $$ と直すと, $u_{m}$ は$$ u_{m+2} = 2u_{m+1} -2 u_{m} $$ が成り立つ. $u_0 = -1-2i$, $u_1 = -3+i$ から, $m=0\ldots 8$まで,
| ${m}$ | $u_{m}$ | $|u_m|^{2}$ |
|---|---|---|
| $0$ | $-1-2i$ | $5$ |
| $1$ | $-3+i$ | $10$ |
| $2$ | $-4+6i$ | $52$ |
| $3$ | $-2+10i$ | $104$ |
| $4$ | $4+8i$ | $5\times 16$ |
| $5$ | $12-4i$ | $10\times 16$ |
| $6$ | $16-24i$ | $52\times 16$ |
| $7$ | $8-40i$ | $104\times 16$ |
| $8$ | $-16-32i$ | $5\times 16^{2}$ |
とわかり, 特に $u_{m+4} = -4u_{m}$ なので, $s_m = |u_{m}|^{2}$ とおくと, $$ s_{4k} = 5\times 2^{4k}, \quad s_{4k+1} = 5\times 2^{4k+1}, \quad s_{4k+2} = 13\times 2^{4k+2}, \quad s_{4k} = 13\times 2^{4k+3} $$ がわかる. あとはこれが $10^8$ を超えるところを地道に調べれば良い.
いかがでしたか?
しんどい式変形よりも楽しい解法にはなったと思う.
そういえば, $\alpha=\beta$ のときは, $$ x_n = \alpha^{n} (c_1 n +c_2) $$ が一般解になりますね.