
スリンキーコイルは面白いおもちゃです. 今回はそれに関する物理オリンピックの教材の問題についてです.
問題 - Kevin M4 Q23 より
$N$ 個の同一の質点$\; m $ がバネ定数 $k$ のバネで繋がれている. このとき, $N$ 個の質点の固有振動数(基準モード)を求めよ.

解いてみた
もとの教材には小問がついています. まず $N=2$ の場合を考えましょう. 質点の番号を上から時計回りに $0$, $1$, $\ldots$, $N-1$ とします.
$N=2$ のとき
$2$ 個の質点の基準点からの変位を $y_0$, $y_1$ とします.
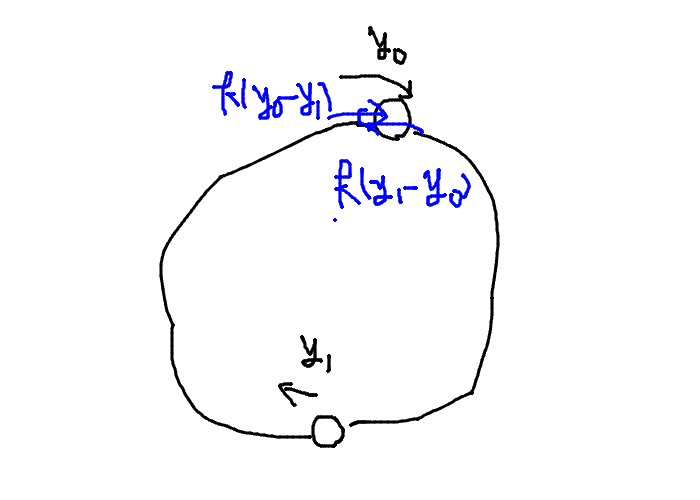
質点$0$ と $1$ の間にあるばねは $y_1-y_0$ 伸びていて, $1$ と $0$ にあるばねは $y_0-y_1$ 伸びているので, 質点の運動方程式は \begin{aligned} & m\ddot{y_0} = k(y_1-y_0) - k(y_0-y_1) \\ & m\ddot{y_1} = k(y_0-y_1) - k(y_1-y_0) \\ \end{aligned} となります. これらを整理すると, \begin{aligned} & \ddot{y_0}+\ddot{y_1} = 0 \\ & \ddot{y_0}-\ddot{y_1} = -\frac{4k}{m} (y_0-y_1) \\ \end{aligned} と, $y_0$, $y_1$ は等速の並進運動か (この場合は角振動数 $\omega = 0$ ), 角振動数 $\sqrt{\frac{4k}{m}}$ の単振動になります. 後者の場合, $\ddot{y_0}+\ddot{y_1}=0$ なので, $y_0$ と $y_1$ は逆位相でなければなりません. つまり, 次のような運動が固有振動です.
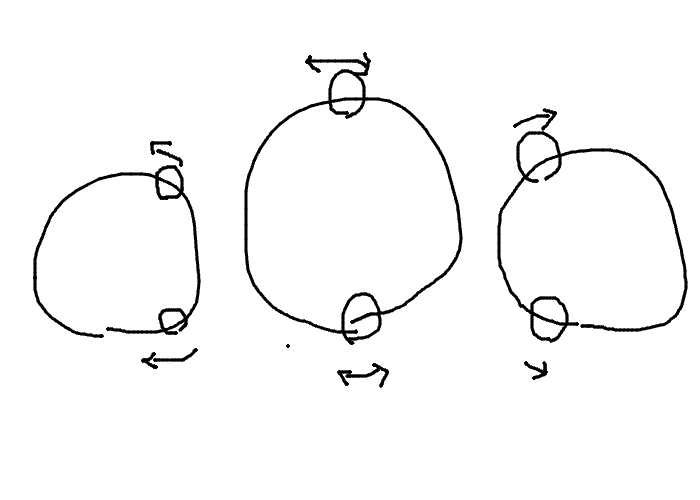
その振動数は, ばねの単振動の振動数 $\omega_0 = \sqrt{\frac{k}{m}}$ を基準にすると, $$ \omega = 2\omega_0 $$ となります.
$N=3$ のとき
先ほどと同様に運動方程式を立てると, \begin{aligned} & m\ddot{y_0} = k(y_1-y_0) - k(y_0-y_2) \\ & m\ddot{y_1} = k(y_2-y_1) - k(y_1-y_0) \\ & m\ddot{y_2} = k(y_0-y_2) - k(y_2-y_1) \\ \end{aligned} となります. これら3本の式を足すと, $\omega=0$ のモードに対応する $$ \ddot{y_0} +\ddot{y_1}+\ddot{y_2} =0 $$ が出てきます. また, 1本目から2本目の式を引くと, $$ \ddot{y_0} - \ddot{y_1} = -\frac{3k}{m} (y_0-y_1) $$ となり, これは $\sqrt{3}\omega_0$ の角振動数を与えます.
振動モードは線型独立なものが合計3つあります. (自由度の数だけ存在する) まずは並進の1つに加え, $\omega=\sqrt{3}\omega_0$ のものは複素数 $z_1$, $z_2$ を用いて $$ y_0 = e^{i\omega t}, \quad y_1 = z_1 e^{i\omega t}, \quad y_2 = z_2 e^{i\omega t} $$ と解を予想すると, もとの方程式は \begin{aligned} & 3 = 2 -z_2-z_1 \\ & 3z_1 = 2z_1 - 1 -z_2 \\ & 3z_2 = 2z_2 - z_1 - 1 \\ \end{aligned} がとなります. これらの解は不定で, $z_1+z_2 = 1$ なる解を任意に2つ独立に取ることができます. ここではわざとらしく, $$ (z_0,z_1,z_2) = \left(1,\frac{-1+\sqrt{3}i}{2}, \frac{-1-\sqrt{3}i}{2}\right), \left(1,\frac{-1-\sqrt{3}i}{2}, \frac{-1+\sqrt{3}i}{2} \right) $$ が2つの独立な振動モードで, 任意の系の振動はこれらの線型結合で表現できます.
また, 振動数を求める方法で機械的なものがあります. これは昨年の選抜でも出題されていましたが, $$\textbf{A} = \begin{pmatrix} 2 & -1 & -1 \\ -1 & 2 & -1 \\ -1 & -1 & 2 \\ \end{pmatrix} $$ とすると, $$ \begin{pmatrix} \ddot{y_0} \\ \ddot{y_1} \\ \ddot{y_2} \end{pmatrix} = -\omega_0^2 \textbf{A} \begin{pmatrix} y_0 \\ y_1 \\ y_2 \end{pmatrix} $$ となり, 振動数 $\omega$ での振動をする場合 $$ \begin{pmatrix} \ddot{y_0} \\ \ddot{y_1} \\ \ddot{y_2} \end{pmatrix} = -\omega^2 \begin{pmatrix} y_0 \\ y_1 \\ y_2 \end{pmatrix} $$ を満たすので, これらを連立させると, 方程式$$ - \omega_0^{2} \textbf{A} \begin{pmatrix} \ddot{y_0} \\ \ddot{y_1} \\ \ddot{y_2} \end{pmatrix} = -\omega^2 \begin{pmatrix} \ddot{y_0} \\ \ddot{y_1} \\ \ddot{y_2} \end{pmatrix} $$ となり, これが $y$ について $0$ でない解を持つためには, $$ \det \textbf{A}' = 0 $$ ただし, $\omega / \omega_0 = x$ として, $$ \textbf{A}' = \begin{pmatrix} 2-x^2 & -1 & -1 \\ -1 & 2-x^2 & -1 \\ -1 & -1 & 2-x^2 \\ \end{pmatrix} $$ となります. これを計算すると, $$ (2-x^2)^3 - 3(2-x^2) +2=0 $$ となるので, 因数分解できて, $$ (3-x^2)^2 (x^2) = 0 $$ となるので, $\omega = \sqrt{3}\omega_0 , 0 $ が固有振動数になります.
一般の $N$ のとき
先ほどの方法を使うと, $N$ 点の質点についての固有振動数は, $\omega / \omega_0 = x$ とおくと, $x$ は $$ \det \begin{pmatrix} 2-x^2 & -1 & 0 & \cdots & 0 & -1 \\ -1 & 2-x^2 & -1 & \cdots & 0 & 0 \\ 0 & -1 & 2-x^2 & \ddots & \vdots & \vdots \\ \vdots& \vdots& \ddots& \ddots & -1 & 0 \\ 0 & 0 & \cdots& -1 & 2-x^2& -1 \\ -1 & 0 & \cdots& 0 & -1 & 2-x^2 \end{pmatrix}_{N\times N}=0 $$ を満たせば良いことになりますが, これを計算するのはしんどいです.
振動モードを $N$ 個求めさえすれば良いので, 並進の $1$ 個と合わせてそれを予想します. さきほど得た $N=2,3$ の結果から予測すると, おそらく次のような解が予測できます. $$ y_j = e^ {i\left(\omega t + j\phi_n \right)} \qquad ( j = 0,1,\ldots , N-1). $$ ただし $\phi_n = \frac{2\pi n}{N} \quad (n = 1,2,\ldots N-1) $ です. この解が方程式を満たすか確認します. どれを代入しても同じなので, $j=0$ の方程式は, $$ -\omega^2 e^{i\omega t} = -\omega_0^2 ( 2 - e^{i\phi_n} - e^{-i\phi_n} ) e^{i\omega t} $$ となるので, $$ \frac{\omega^2}{\omega_0^2} = 2 - 2\cos\left(\frac{2\pi n}{N}\right) $$ つまり, $2-2\cos x = 4\sin^2\frac{x}{2}$ なので $$ \omega = 2\omega_0 \sin\frac{\pi n}{N} \qquad n = 1,2,\ldots N-1 $$ とすると, 条件をみたします.
まず振動数が違うものは線型独立なモードで, 振動数が同じ $n$ と $N-n$ に関しては複素共役 ( 時間が逆向き ) に振動しているので, 定数倍で表せず, したがってこれら $N-1$ 個のモードは全て線型独立で, 無事 $N$ 個のそれが見つかりました. 固有角振動数は $$
\omega = 2\omega_0 \sin\frac{\pi n}{N} \qquad n = 0,1,\ldots N-1
$$
という奇妙な値をとります.
ふかぼる
固有振動数の取りうる値は離散的で, なぜか範囲があります. これはどういうことなのでしょうか.
$N \to \infty$ で考察したいです. これは冒頭で見せたスリンキーコイルのような状況になっています. 前の方法で見つけた固有振動モードは, $j$ が進むと位相がちょっとずつずれていって, 一周すると $n$ 個の波が入っていることになります. (位相が $2\pi n$ ずれるので. )

これを境界条件が課された波動方程式に直したいですが, あいにくバネ定数 $k$ は長さの逆数に依存するなど扱いづらいです. ここで, バネの材質によらないヤング率 $E$ ? みたいなものとバネの断面積みたいなもの $A$, バネの長さ $\ell$ を用いて $$ k = \frac{EA}{\ell} $$ と表します. $E$ は材質によるものとし, $A$ は一定なので $EA=F$ とおいておきます.
いま, スリンキーコイルの一周の長さが $L$, 質量が $M$ であるとします. このとき, 適当な大きな整数 $N$ を用いて, これを $N$ 個の質量 $m = \frac{M}{N}$ の質点と $N$ 本の長さ$\ell=\frac{L}{N}$, ばね定数 $k = \frac{F}{\ell}$ のばねで繋がれているとモデル化すると, $j$ 番目の基準点からの変位 $y_j$ は, 先ほどの運動方程式と同じで, $$ m\ddot{y_j} = k ( y_{j+1} - 2y_{j} + y_{j-1}) $$ となり, これの両辺を $m$ で割ると $$ \frac{\partial^2 y_j}{\partial t^2} = \frac{k\ell^2}{m} \frac{y_{j+1} - 2y_{j} + y_{j-1}}{\ell^2} $$ となり, バネの長さに沿った座標 $x$ を取って, $\ell \to 0$の極限を取ると, $$ \frac{\partial^2 y_j}{\partial t^2} = \frac{k\ell^2}{m} \frac{\partial^2 y_j}{\partial x^2} $$ と, 変位$y$ の波動方程式に直せました. この波の位相速度 $v$ は, $$ v^2 = \frac{k\ell^2}{m} = \frac{F}{\ell} \frac{\ell^2}{m} = F\cdot \frac{L}{N} \cdot \frac{N}{M} = \frac{FL}{M} $$ と, $v= \sqrt{\frac{FL}{M}}$ と, $N$ に依存しない形になります.
ここで, 波が 長さ $L$ 中に $n$ 個入っている状況を考えると, その固有振動数は, $N$ を適当に取ると $$ \omega_n = 2\omega_0 \sin \left(\frac{\pi n}{N} \right) $$ でした. $\omega_0$ は全然定数ではなく, $$ \omega_0 = \sqrt{\frac km} = \sqrt {\frac{F}{LM}} N $$ なので, $N\to \infty$ の極限を取ると, $$ \omega_n = 2\sqrt{\frac{F}{LM}} \; N \cdot \frac{\pi n}{N} = 2\pi \sqrt{\frac{F}{LM}} n $$ となるので, 一波長の長さ$\lambda$は $$ \lambda = \frac{v}{\omega / 2\pi} = \frac{ \sqrt{\frac{FL}{M}} } { \sqrt{\frac{F}{LM}} n} = \frac{L}{n} $$ と, 確かに一致しています.
いかがでしたか?
なんかよくわからない結論になってしまった.